Artigo escrito com a colaboração de Bruna Faria
Este é um artigo para atender uma dúvida que surge em muitos pesquisadores quando se deparam com o Boxplot.
Nas mais diversas áreas do conhecimento, medidas de posição e variação relativa são comumente utilizadas na análise exploratória de variáveis quantitativas ou ordinais. Medidas como a média, desvio-padrão, mínimo, primeiro quartil, segundo quartil, terceiro quartil e máximo são as principais e mais comuns medidas descritivas para estes tipos de variáveis.
Estas medidas podem ser apresentadas também em disposições gráficas, como é o caso do boxplot, por exemplo.
Mas antes de dar início à explicação e interpretação do boxplot, vamos fazer uma breve explicação sobre os quartis, que são medidas apresentadas no boxplot.
Leia também: O que é desvio-padrão? E erro-padrão?
O que são quartis? Qual a diferença entre quartil e percentil?
Para que fique clara a breve explicação, vamos começar definindo os percentis. O percentil é uma medida de posição que, dada uma amostra ordenada em ordem crescente e dividida em 100 partes, indica o valor do qual determinado percentual de elementos da amostra são menores ou iguais a ele.
Para exemplificar, vamos tomar a idade de 12 indivíduos e ordenar em ordem crescente.
| Posição | Idade |
| 1 ª | 18 |
| 2 ª | 19 |
| 3 ª | 21 |
| 4 ª | 21 |
| 5 ª | 21 |
| 6 ª | 22 |
| 7 ª | 22 |
| 8 ª | 22 |
| 9 ª | 23 |
| 10 ª | 23 |
| 11 ª | 24 |
| 12ª | 27 |
Como calcular o percentil 25 dessa amostra?
Bom, queremos então saber qual o valor tal que 25% dos dados são menores ou iguais a ele. Para encontrar o percentil 25, primeiramente precisamos encontrar em qual posição devemos buscar o valor. Chegamos a essa posição, multiplicando o percentil que queremos pelo tamanho da amostra e dividindo por 100.
Posição do Percentil 25 = Percentil * Tamanho da Amostra / 100 = 25 * 12 / 100 = 300/100 = 3
Na posição 3, temos a idade de 21 anos. Sendo assim, o percentil 25 dessa amostra é 21 anos. Isso significa que pelo menos 25% dos indivíduos dessa amostra tem no máximo 21 anos.
E se o cálculo da posição de determinado percentil não resultar em um número inteiro? Nesse caso, o ideal é que seja feita uma interpolação. Não entraremos em detalhes e deixaremos isso para um futuro artigo sobre medidas descritivas de posição.
E os quartis?
Os quartis nada mais são que os percentis 25, 50 e 75, representando respectivamente o primeiro, segundo e terceiro quartil. Veja que o segundo quartil equivale ao percentil 50, valor em que pelo menos 50% da amostra está acima dele e pelo menos 50% está abaixo. Não é isso a definição de mediana? Sim! O percentil 50 ou segundo quartil equivalem à mediana!
Agora que pincelamos o conceito de percentis, quartis e mediana, vamos ao ponto de interesse do artigo.
O que é o boxplot? Como ele é formado?
O boxplot ou diagrama de caixa é uma ferramenta gráfica que permite visualizar a distribuição e valores discrepantes (outliers) dos dados, fornecendo assim um meio complementar para desenvolver uma perspectiva sobre o caráter dos dados. Além disso, o boxplot também é uma disposição gráfica comparativa.
As medidas de estatísticas descritivas como o mínimo, máximo, primeiro quartil, segundo quartil ou mediana e o terceiro quartil formam o boxplot.
Observe a figura do boxplot. Note que o local onde a haste vertical começa (de baixo para cima) indica o mínimo (excetuando algum possível valor extremo ou outlier) e, onde a haste termina indica o máximo (também excetuando algum possível outlier).

O retângulo no meio dessa haste possui três linhas horizontais: a linha de baixo, que é o próprio contorno externo inferior do retângulo, indica o primeiro quartil. A de cima, que também é o próprio contorno externo superior do retângulo, indica o terceiro quartil. A linha interna indica o segundo quartil ou mediana.
Os asteriscos ou pontos que ás vezes aparecem no boxplot indicam que aquelas observações são atípicas, valores discrepantes, extremos ou outliers.
Como interpretar o boxplot?
O boxplot nos fornece uma análise visual da posição, dispersão, simetria, caudas e valores discrepantes (outliers) do conjunto de dados.
- Posição – Em relação à posição dos dados, observa-se a linha central do retângulo (a mediana ou segundo quartil).
- Dispersão – A dispersão dos dados pode ser representada pelo intervalo interquartílico que é a diferença entre o terceiro quartil e o primeiro quartil (tamanho da caixa), ou ainda pela amplitude que é calculada da seguinte maneira: valor máximo – valor mínimo. Embora a amplitude seja de fácil entendimento, o intervalo interquartílico é uma estatística mais robusta para medir variabilidade uma vez que não sofre influência de outliers.
- Simetria – Um conjunto de dados que tem uma distribuição simétrica, terá a linha da mediana no centro do retângulo. Quando a linha da mediana está próxima ao primeiro quartil, os dados são assimétricos positivos e quando a posição da linha da mediana é próxima ao terceiro quartil, os dados são assimétricos negativos. Vale ressaltar que a mediana é a medida de tendência central mais indicada quando os dados possuem distribuição assimétrica, uma vez que a média aritmética é influenciada pelos valores extremos.
- Caudas – As linhas que vão do retângulo até aos outliers podem fornecer o comprimento das caudas da distribuição.
- Outliers – Já os outliers indicam possíveis valores discrepantes. No boxplot, as observações são consideradas outliers quando estão abaixo ou acima do limite de detecção de outliers.
O limite de detecção de outliers é construído utilizando o intervalo interquartílico, dado pela distância entre o primeiro e o terceiro quartil. Sendo assim, os limites inferior e superior de detecção de outlier são dados por:
- Limite Inferior = Primeiro Quartil – 1,5 * (Terceiro Quartil – Primeiro Quartil)
- Limite Superior = Terceiro Quartil + 1,5 * (Terceiro Quartil – Primeiro Quartil)
Construindo um boxplot no R
Vamos tomar como base nossa tabela de dados de idade, utilizada anteriormente. Ela nos fornece as seguintes medidas descritivas:
| Variável | Mínimo | 1º Quartil | 2º Quartil | 3º Quartil | Máximo |
| Idade | 18 | 21 | 22 | 23 | 27 |
Segue então, o passo a passo para construir o boxplot no R:
# Primeiro criamos a variável Idade > Idade <- c(21,22,24,18,19,27,22,22,23,21,23,21) # Depois, podemos usar a função summary(variável) para verificar as medidas descritivas da variável > summary(Idade) Min. 1st Qu. Median Mean 3rd Qu. Max. 18.00 21.00 22.00 21.92 23.00 27.00 # Em seguida, usamos a função boxplot(variável, main="título do grafico", col="cor do gráfico") para construir o gráfico. > boxplot(Idade, main="Boxplot: Idade", col="blue")
Resultado:
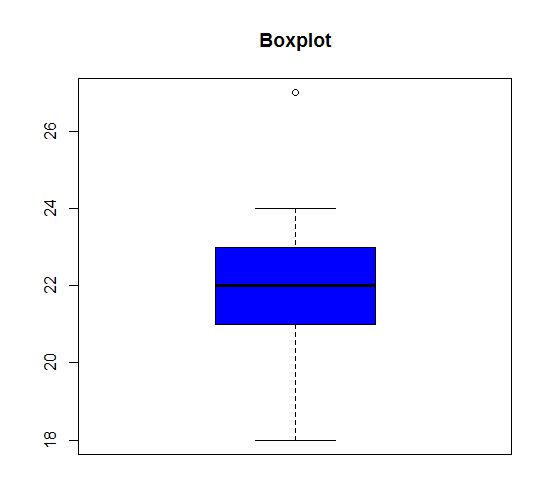
Neste segundo exemplo vamos apresentar o boxplot comparativo. Como dito anteriormente, o boxplot é uma ferramenta gráfica comparativa entre grupos com relação à posição, à dispersão e à distribuição dos dados.
Utilizaremos o banco de dados “cats” do pacote “MASS” do R. Esse banco de dados contém dados de gatos adultos, pesando mais de 2 kg. Utilizaremos as variáveis peso corporal (“Bwt”) e sexo (“Sex”) para construir o boxplot comparativo.
> require(MASS)
Carregando pacotes exigidos: MASS
> data(cats)
> boxplot(cats$Bwt~cats$Sex, main="Boxplot Comparativo: Peso x Sexo", col=c("red", "blue"))
Resultado:
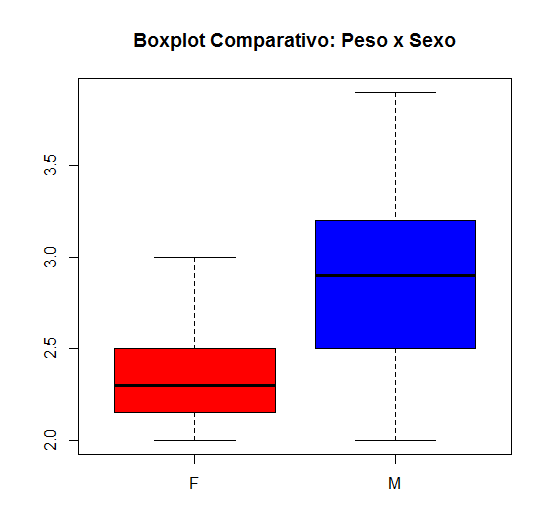
Com o boxplot comparativo podemos concluir, por exemplo, que o peso corporal dos gatos do sexo masculino apresentam maior variabilidade que o peso corporal dos gatos do sexo feminino.
Gostou do nosso artigo sobre o Boxplot? Caso ainda tenha ficado alguma dúvida, entre em contato com nossos Data Talkers e não deixe de assinar nosso Blog para acompanhar nossas futuras publicações.




33 comentários em “Boxplot: Como interpretar?”
muito interessante seus conteúdos gostei muito deles. Parabéns 🙂
Muito obrigada Mirela! Segue a gente nas redes sociais pra não perder nenhuma postagem.
Já naveguei todo o site e temas do blog. As abordagens que vocês fazem são muito esclarecedoras. Essa sobre boxplot, me ajudou a entender melhor e tirou minhas dúvidas. Parabéns!!
Vocês poderiam falar sobre Tamanho de Amostras?
Ei João, que bom que você curtiu nossos artigos!
Anotamos aqui a sua sugestão e em breve teremos artigo sobre o assunto. Continua seguindo a Oper nas redes sociais para ficar por dentro das novidades! Sempre divulgamos os artigos novos no Instagram, Facebook e LinkedIn
Excelente conteúdo! Está me ajudando muito na escrita da minha tese de doutorado. Outras fontes onde busquei informações sobre boxplot traziam apenas explicações superficiais. Muito obrigado!
Que ótimo Felipe, ficamos felizes em ajudar! Se precisar de um suporte extra, entra em contato com a gente 😀
Muitissimo obrigada! Me ajudou muito! A escrita é bem clara! Muito grata!
Valeu Patricia! 😀
Pingback: Gerei meus dados. E agora? – Press a button
Muoto bom
Está ajudando muito. Parabéns pela clareza e completude!
Valeu Augusto!
Excelente conteúdo, parabéns! Tem me ajudado muito nos meus estudos 😀
Que ótimo Jamilla, ficamos felizes em saber! 😀 Acompanhe as nossas redes sociais, sempre postamos os artigos novos por lá.
Excelentes explicações. Ajudaram bastante, Continuem assim
Valeu Rômulo! 🙂
O que pode se concluir quando a mediana é igual ao 3º quartil?
Oi José, quando a mediana é igual ao terceiro quartil significa que você deve ter muitos dados repetidos e possivelmente uma assimetria à esquerda.
Muito bom o conteúdo, parabéns! Estou com uma dúvida: devo procurar por valores outliers em todo conjunto de dados (machos e fêmeas agrupados) ou dentro de cada sexo, antes de prosseguir uma análise de variância?
Boa pergunta, Adalfredo! Geralmente não excluímos outliers, buscamos análises capazes de comportar valores extremos e só excluímos outliers se tivermos evidências de que são um erro. Se tiver um tamanho grande de amostra em cada um dos sexos pode encontrar outliers pelos sexos, mas se não tiver uma amostra tão grande assim, aconselhamos fazer de forma geral.
Olá, no seu primeiro boxplot, o limite de detecção do outlier superior não deveria ser 26?
Limite superior + 1,5 * (3ºquartil – 1 º quartil)= 23 + 1,5 * 2 = 26
Oi Thales! O limite superior para o dado ser considerado um outlier é 26 mesmo, mas, se você olhar no banco de dados, o único valor maior ou igual a 26 é 27. E é ele que vai ser ilustrado no boxplot pela bolinha.
Olá. O limite de detecção outlier é 26. Logo o 27 é outlier( bolinha). Mas não entendi qual o valor que está como máximo no bloxpot. Pra mim não faz sentido. Alguém poderia explicar?
Oi Allan! As bolinhas servem para detectar outlier, ou seja, acima ou abaixo dela é um outlier. Se não tiver outlier, os valores das bolinhas serão o de máximo e mínimo. Se tiver outliers, o mais extremo acima do boxplot vai assumir valor de máximo e o outlier mais extremo abaixo do boxplot vai assumir o valor de mínimo.
Olá. O que estou dizendo é que não entendi o valor do ghráfico de maximo estar em 24( pelo que parece) se o maximo, pelos dados é 27.
Olá, após a leitura eu fiquei com duvida da minha performance. Fiz o grafico usando dados de resultado financeiro de meus trades. (compra e venda de contratos futuros de dolar).amostragem é pequena 260 eventos. Eu pensei que estava indo bem pois a mediana está se arpoximando do 3º quartil. Mas pelo texto entendo que estou indo pra negativo? “Quando a linha da mediana está próxima ao primeiro quartil, os dados são assimétricos positivos e quando a posição da linha da mediana é próxima ao terceiro quartil, os dados são assimétricos negativos”
Foto do grafico https://prnt.sc/vo0erd obrigado
Olá Eric. Não fique com dúvidas sobre a sua performance. Se a distribuição dos seus trades tem assimetria negativa, isso é um bom sinal. Talvez o que tenha te deixado confuso seja o conceito de assimetria positiva e negativa. Olha essa imagem aqui de exemplo: https://operdata.com.br/wp-content/uploads/2021/01/Assimetria-positiva-e-negativa.jpeg
O valor máximo e mínimo do box plot, são os valores máximos e mínimos dos dados estabelecidos (rol)?
Oi Pedro! Os valores máximos e mínimos de um boxplot serão os maiores e os menores valores dos dados analisados respectivamente. Podendo inclusive ser outliers. O boxplot auxilia na identificação de pontos fora da curva.
Gostei muito do artigo e, deu para esclarecer as minhas dúvidas. Parabéns!
Fiz um boxplot, mas o valor do 3º quartil deu similar a mediana, é correto, como interpreto? sendo que visualmente só aparecerão dois valores, o do 1º quartil, e, o da mediana e 3º quartil que são os mesmos valores.
Sim, é possível que o valor do terceiro quartil seja igual ao valor da mediana em um boxplot. Na verdade, quando isso acontece, significa que a distribuição dos dados é simétrica.
Interpretando o seu boxplot, você pode dizer que metade dos dados estão abaixo da mediana e metade acima. Além disso, você sabe que a distribuição dos dados é simétrica, ou seja, há uma quantidade igual de valores abaixo e acima da mediana.
Vale lembrar que, mesmo que haja apenas dois valores visíveis no boxplot (primeiro quartil e mediana/terceiro quartil), ainda existem dados abaixo do primeiro quartil e acima do terceiro quartil, que são representados pelos pontos fora dos limites do boxplot (chamados de “outliers”). Esses outliers podem ser importantes para entender melhor a distribuição dos seus dados e podem ser investigados mais a fundo.
Parabénsss, ótimo artigo!