No artigo “Como interpretar uma análise de variância?” vimos que para utilizar ANOVA é necessário que algumas suposições, como a de normalidade e variância constante dos resíduos, sejam validadas. Mas o que fazer quando estas suposições não são atendidas? Um caminho alternativo é a utilização do teste de Kruskal-Wallis.
Em diversas áreas do conhecimento, principalmente nas ciências sociais e humanas, é comum encontrar a aplicabilidade de testes não-paramétricos. Neste artigo, abordaremos os testes de Kruskal-Wallis e Nemenyi para comparações múltiplas.
o teste de Kruskal-Wallis
O teste de Kruskal-Wallis é uma extensão do teste de Wilcoxon-Mann-Whitney. Enquanto o teste não paramétrico de Wilcoxon-Mann-Whitney consiste em comparar a distribuição de duas amostras, o teste de Kruskal-Wallis permite realizar a comparação de três ou mais grupos em amostras independentes.
Por isso, o teste de Kruskal-Wallis é o método não-paramétrico alternativo à ANOVA para um fator (Kruskal e Wallis, 1952), sendo utilizado nos casos em que as suposições exigidas pela ANOVA não são atendidas.
Para utilizar o teste de Kruskal-Wallis é necessário que as variáveis sejam quantitativas ou estejam, pelo menos, em escala ordinal (como por exemplo variáveis medidas em escala likert).
| Comparação de variável quantitativa | Teste paramétrico | Teste não-paramétrico |
| Entre dois grupos | Teste t | Teste Mann-Whitney |
| Entre três ou mais grupos | ANOVA | Teste de Kruskal-Wallis |
| Comparações múltiplas | Teste de Tukey | Teste de Nemenyi |
Qual a diferença entre o teste de Kruskal-Wallis e ANOVA?
A principal diferença entre os testes se deve ao fato de que para fazer a ANOVA devemos validar as suposições de normalidade, variância constante e independência dos resíduos e que as variáveis devem ser do tipo contínuas. Já para a realização do teste de Kruskal-Wallis devemos considerar apenas a suposição de que as observações sejam independentes e que as variáveis sejam do tipo contínuas ou ordinais.
Além disso, enquanto a ANOVA testa a média e a variação entre os grupos (fatores), o teste de Kruskal-Wallis consiste em testar uma pseudo-mediana.
Pseudo-mediana? Afinal, o que o teste de Kruskal-Wallis testa?
Como dito anteriormente, o teste de Kruskal-Wallis é análogo à ANOVA e consiste em testar uma pseudo-mediana. Mas a rigor, o teste de Kruskal-Wallis avalia diferenças de médias de ordens (postos), as quais não são necessariamente iguais às medianas dos grupos, uma vez que é atribuído a cada observação seu posto (ordem).
Mas, antes disso, deve-se ordenar as observações em ordem crescente, independente dos grupos, e em seguida fazer a distribuição dos postos, onde o menor valor recebe o posto ou ordem 1, o segundo 2 e assim sucessivamente, até que todas as observações tenham sido consideradas.
Quando há observações repetidas, é indicado que seja atribuído o valor médio dos postos entre estas observações. Por isso, pode ocorrer do resultado do teste apontar para a diferença significativa entre os grupos, mas as medianas serem iguais ou relativamente próximas. Quando isso ocorre, o teste de Kruskal-Wallis testa, em simultâneo, a mediana e as formas de distribuição.
Quando os grupos apresentam a mesma forma de distribuição de probabilidade, o resultado do teste de Kruskal-Wallis pode ser interpretado com base na mediana.
Aplicação do teste de Kruskal-Wallis
Vamos supor um experimento que foi elaborado com o objetivo de verificar o comportamento do peso de tomates italianos cultivados em solos enriquecidos com diferentes tipos de nutrientes.
Quatro solos foram enriquecidos com diferentes nutrientes e nomeados como “A”, “B”, “C” e “D”. Em seguida foram cultivados tomates italianos e, após o período de crescimento, foram colhidos e pesados seis tomates de cada solo.

| Grupo | Peso dos tomates italianos colhidos (em gramas) | |||||
| Solo “A” | 128,5 | 162,8 | 111,4 | 128,5 | 205,7 | 128,5 |
| Solo “B” | 128,5 | 102,8 | 102,8 | 179,9 | 248,5 | 137,1 |
| Solo “C” | 162,8 | 137,1 | 68,6 | 98,5 | 77,1 | 137,1 |
| Solo “D” | 85,7 | 102,8 | 111,4 | 77,1 | 60 | 68,6 |
Em nosso exemplo, podemos definir as hipóteses do teste como:
- H0: Não existe diferença entre o peso do tomate italiano cultivado nos quatro solos.
- H1: Há pelo menos um solo com o peso do tomate italiano cultivado diferente.
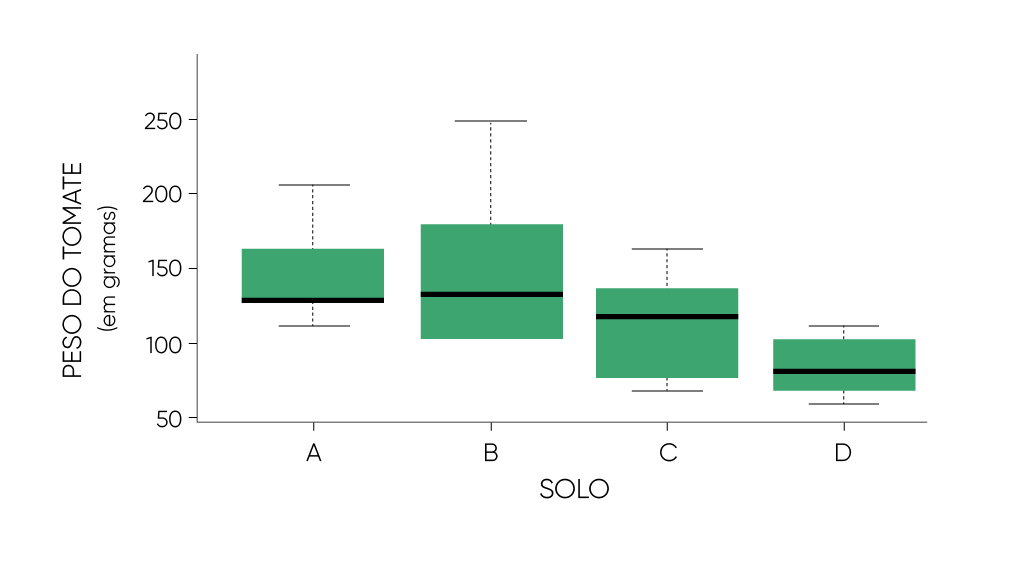
No boxplot abaixo pode-se visualizar o comportamento do peso dos tomates italianos cultivados em cada um dos quatro solos.
Essa aparente diferença do pesos dos tomantes cultivados nos diferentes solos é significativa?
Vamos entrar com os dados no R e utilizar o teste Kruskal Wallis para responder à essa questão.
> peso <- c(128.5, 162.8, 111.4, 128.5, 205.7, 128.5, 128.5, 102.8, 102.8, 179.9, 248.5, 137.1, 162.8, 137.1, 68.6, 98.5, 77.1, 137.1, 85.7, 102.8, 111.4, 77.1, 60, 68.6)
> cultivo <- c(rep("A",6),rep("B",6),rep("C",6),rep("D",6))
> kruskal.test(peso~factor(cultivo))
Kruskal-Wallis rank sum test
data: peso by factor(cultivo)
Kruskal-Wallis chi-squared = 9.0028, df = 3, p-value = 0.02925
O p-valor do teste de Kruskal-Wallis de 0,029 (menor que um nível de significância de 0,05) nos leva a rejeitar a hipótese nula de que não existe diferença entre o peso dos tomates italianos cultivados nos diferentes solos.
Mas como saber em quais solos o peso dos tomates se diferem?
Quando aplicamos a ANOVA para comparar os grupos e obtemos um resultado que indica que pelo menos dois grupos se diferem entre si, utilizamos o teste de Tukey para comparações múltiplas.
Já ao utilizar o teste de Kruskal-Wallis, o teste de comparações múltiplas adequado é o de Nemenyi.
Teste de comparação múltipla de Nemenyi
O teste de Nemenyi (Nemenyi, 1963) é um teste post-hoc, ou seja, é um teste de comparação múltipla que é usado após a aplicação de teste não paramétricos com três ou mais fatores, como por exemplo, o teste de Kruskal-Wallis.
O teste consiste em fazer comparações em pares com o intuito de verificar qual dos fatores que diferem entre si. No entanto, o teste de Nemenyi é muito conservador e pode não encontrar diferença significativa entre os pares testados.
O pacote PMCMR do R, possui a função posthoc.kruskal.nemenyi.test() para se realizar o teste de comparação múltipla de Nemenyi.
> posthoc.kruskal.nemenyi.test(peso ~ factor(cultivo))
Pairwise comparisons using Tukey and Kramer (Nemenyi) test
with Tukey-Dist approximation for independent samples
data: peso by factor(cultivo)
A B C
B 1.000 - -
C 0.663 0.713 -
D 0.044 0.055 0.456
Avaliando os p-valores das comparações duas a duas, podemos ver que o teste só revelou haver diferença significativa entre o peso dos tomates cultivados nos solos A e D (p-valor = 0,044). O teste não apresentou evidências de diferença significativa entre o peso dos tomates cultivados nos solos A e B (p-valor = 1,000), A e C (p-valor = 0,663), B e C (p-valor = 0,713), B e D (p-valor = 0,055) e entre os tomates cultivados nos solos C e D (p-valor = 0,456).
Agora que você sabe um pouco mais sobre a utilização dos testes não paramétricos de Kruskal-Wallis e Nemenyi para comparações múltiplas, siga-nos nas redes sociais para saber quando saem as novas publicações. Em caso dúvidas ou sugestões, comente aqui em baixo!
Artigo desenvolvido com a colaboração de Bruna Faria.




5 comentários em “Teste de Kruskal-Wallis e Nemenyi”
Ótima didática, parabéns. Muito útil o artigo. Obrigado.
Valeu, Marcio!
boa
E quando KW tem p<0,05, mas o post hoc não exibe diferenças entre os tratamentos? Acontece comigo. Como explicar?
Bom dia, Wanderson!
O KW e o POST HOC são coisas diferentes e não deveriam obrigatoriamente dar os mesmos resultados, da mesma forma que quando testamos normalidade com testes diferentes podemos ter resultados diferentes sobre rejeitar ou não a hipótese nula. Pra isso acontecer, imagino que o p valor é bem próximo de 0.05, ou seja, está no limiar pra ser significativo. Também seria interessante saber se existem muitos fatores sendo comparados.