A Análise de Componentes Principais ou PCA (Principal Component Analysis) é uma técnica de análise multivariada que pode ser usada para analisar inter-relações entre um grande número de variáveis e explicar essas variáveis em termos de suas dimensões inerentes (Componentes).
O objetivo é encontrar um meio de condensar a informação contida em várias variáveis originais em um conjunto menor de variáveis estatísticas (componentes) com uma perda mínima de informação.
O número de componentes principais se torna o número de variáveis consideradas na análise, mas geralmente as primeiras componentes são as mais importantes já que explicam a maior parte da variação total.
As componentes principais em geral são extraídas via matriz de covariância, mas também podem ser extraídas via matriz de correlação.
Extraindo as Componentes Principais
Quando se utiliza a matriz de covariância para extração, as componentes são influenciadas pelas variáveis de maior variância. Sendo assim, quando existe uma discrepância muito acentuada entre as variâncias, as componentes principais acabam sendo de pouca utilidade, uma vez que cada componente tende a ser dominada por uma variável.
Em muitos casos, isso ocorre devido às diferenças existentes nas escalas e unidades de medidas das variáveis. Quando isso ocorre deve-se utilizar a matriz de correlação para extrair as componentes para que as variáveis de maior escala numérica não “roubem” a importância da componente para si.
Existem diversas funções para realizar a Análise de Componentes Principais no R, como por exemplo:
- Função: prcomp() – Pacote: stats
- Função: princomp() – Pacote: stats
- Função: PCA() – Pacote: FactoMineR
- Função: dudi.pca() – Pacote: ade4
- Função: acp() – Pacote: amap
Na maioria dessas funções, extrair as componentes principais via matriz de correlação significa padronizar, através do escore Z, as variáveis de interesse. Isso pode ser feito utilizando argumentos já disponíveis nessas funções, uma vez que a matriz de covariância de variáveis padronizadas equivale a matriz de correlação dos dados brutos.
Exemplo de aplicação – Estudo sobre a composição do solo e nível de oxidação da própolis
Suponha um estudo com o interesse de investigar as relações entre elementos químicos do solo (P, K, Ca, Mg, Al, Zn, Fe, Mn, Cu) com o índice de oxidação da própolis.
Decide-se então utilizar a Análise de Componentes Principais para reduzir os elementos do solo em indicadores ou variáveis latentes, passíveis de interpretação, capazes de sintetizar grande parte da variabilidade das variáveis em si.
Utilizando uma das funções apresentadas anteriormente, chega-se ao seguinte resultado:
| Componente | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 | PC7 | PC8 | PC9 |
|---|---|---|---|---|---|---|---|---|---|
| Desvio Padrão | 2,2514 | 1,0022 | 0,9457 | 0,86550 | 0,7054 | 0,6152 | 0,4566 | 0,2401 | 0,0981 |
| Proporção da Variância | 0,6137 | 0,1032 | 0,0917 | 0,0745 | 0,0689 | 0,0358 | 0,0087 | 0,0024 | 0,0011 |
| Proporção Acumulada | 0,6137 | 0,7169 | 0,8086 | 0,8831 | 0,9520 | 0,9878 | 0,9965 | 0,9989 | 1 |
Pode-se notar que as 5 primeiras componentes são capazes de explicar mais de 95% da variabilidade das amostras. Se optássemos por utilizar essas 5 componentes, estaríamos reduzindo o número de 9 variáveis originais para 5 variáveis latentes, perdendo menos de 5% da informação acerca da variabilidade dos dados.
Para criarmos cada variável latente, utilizamos os coeficientes gerados para cada variável original. A partir desses coeficientes se pode compreender o sentido de cada componente extraída na análise.
| VARIÁVEL | PC1 | PC2 | PC3 | PC4 | PC5 |
|---|---|---|---|---|---|
| Fósforo | 0,1781 | 0,6628 | 0,4684 | -0,4507 | 0,0277 |
| Potássio | 0,2757 | -0,3872 | -0,1066 | -0,5906 | -0,4294 |
| Calcio | 0,3879 | 0,1346 | 0,0409 | 0,0971 | 0,2631 |
| Magnésio | 0,3804 | -0,1853 | -0,0926 | 0,1577 | 0,0902 |
| Alumínio | -0,3651 | 0,1026 | -0,0104 | 0,0518 | -0,0226 |
| Zinco | 0,3365 | -0,1725 | -0,1172 | 0,0759 | 0,5037 |
| Ferro | -0,1954 | 0,3221 | -0,7964 | -0,2979 | 0,0639 |
| Manganês | 0,2988 | 0,1700 | -0,0688 | 0,3879 | -0,6872 |
| Cobre | 0,3063 | 0,4279 | -0,3050 | 0,2560 | -0,0330 |
Pode-se entender a relação entre os elementos de cada componente também através de um mapa perceptual.
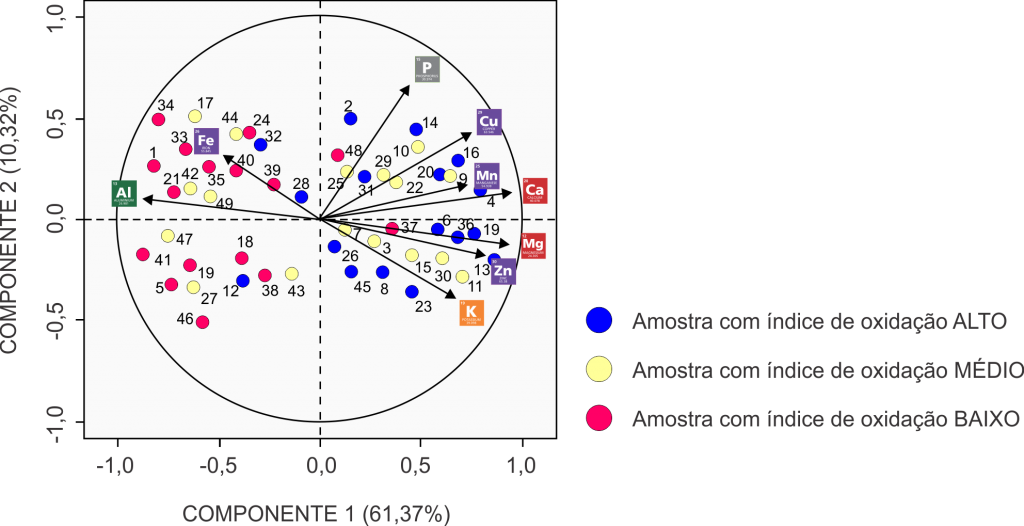
Mapa perceptual – Uma forma de visualizar a relação entre as componentes e as variáveis.
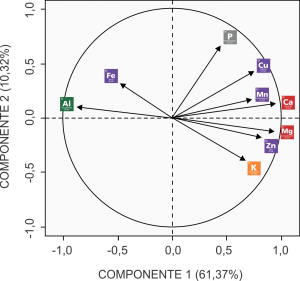
A partir do mapa perceptual, pode-se notar que a primeira componente explica 61,37% da variabilidade dos dados, enquanto que a segunda explica 10,32%. Pode-se considerar que o mapa perceptual bidimensional apresentado está adequado para avaliar as relações entre as variáveis, uma vez que explica grande parte da variabilidade dos dados – geralmente se busca uma explicação maior que 50% nas duas primeiras componentes para usar o mapa.
Pode-se verificar que os elementos Alumínio e Ferro são correlacionados positivamente entre si, o que significa que amostras de solo com alta concentração de Ferro, tendem a apresentar também alta concentração de Alumínio. Ao mesmo tempo, pode-se observar que esses elementos são negativamente correlacionados com os demais, principalmente com Potássio, Zinco e Magnésio.
O mapa perceptual ainda permite identificar como as amostras do solo estão ordenadas e sua relação entre as variáveis. Logo, através da Análise de Componentes Principais pode-se realizar uma espécie de Análise de Agrupamento, sendo que uma das diferenças é que, ao invés de levar em consideração a distância entre as amostras, através de alguma medida de distância como a Euclidiana, estaria se levando em consideração a correlação entre as amostras.
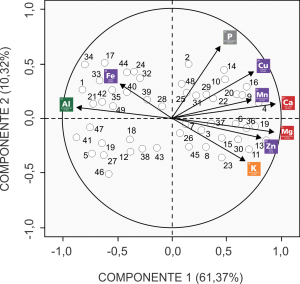
Caracterização das componentes principais
Pensando na construção de indicadores, a primeira componente seria interpretada como uma comparação das concentrações de Alumínio e Ferro com os demais elementos medidos. Logo, quanto menor o valor dessa componente, maiores as quantidades de Alumínio e Ferro em relação aos demais elementos do solo e vice-versa.
A segunda componente pode ser interpretada como um indicador para comparar a concentração dos elementos Potássio, Magnésio e Zinco com os demais componentes do solo e quanto menor os valores desse índice, maiores são as concentrações de Potássio, Magnésio e Zinco em relação a concentração dos demais elementos e vice-versa.
Uso das componentes principais como variáveis latentes
Caracterizadas as componentes, elas podem então ser utilizadas como variáveis latentes para verificar se as mesmas possuem algum tipo de relação com a oxidação da própolis.
Para ilustrar o uso as componentes principais como variáveis latentes, foram elaborados gráficos que representam as médias das duas primeiras componentes, com seus respectivos intervalos de 95% de confiança, nos grupos de amostras em que o nível de oxidação da própolis foi baixo, médio e alto.
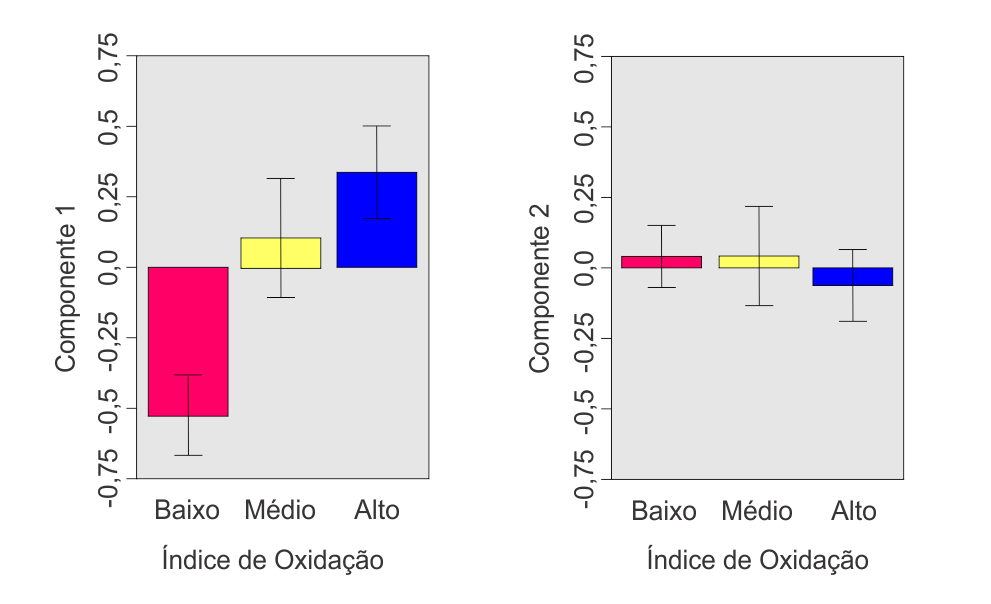
Pode se verificar que, aparentemente, a primeira componente está mais relacionada com a oxidação da própolis que a segunda.
Para melhor investigar essa relação, pode ser realizado um teste de comparação de médias ou outra técnica inferencial. É possível também plotar novamente o mapa perceptual incluindo as amostras classificadas de acordo com seu nível de oxidação.
Solução para problemas frequentes em Análise de Componentes Principais
Em análises que envolvem grande número de variáveis, frequentemente são encontrados autovalores iguais a zero, de forma que a matriz de covariância não seja positiva definida. Isso significa que existem combinações lineares perfeitas entre variáveis. Neste caso, para obter uma matriz de covariância definida positiva, basta eliminar uma das variáveis envolvidas na combinação linear perfeita.
Componentes oriundas de autovalores iguais a zero sempre podem ser eliminados do sistema. No entanto, nesses casos aconselha-se que a análise de componentes principais seja refeita utilizando apenas o número de variáveis igual ao número de autovalores maiores que zero.
Gostou do nosso artigo sobre análise de componentes principais? Assine nossa newsletter para receber todos os conteúdos do nosso blog. E qualquer dúvida sobre a aplicação da técnica ou como funciona a análise de componentes principais, não deixe de entrar em contato com nosso time de Data Talkers.



