O coeficiente de concordância de Kappa é utilizado para descrever a concordância entre dois ou mais juízes quando realizam uma avaliação nominal ou ordinal de uma mesma amostra.
Existem diversas doenças cujos diagnósticos dependem da avaliação do médico dos resultados de exames de imagem. Como exemplo ilustrativo da utilização do coeficiente de Kappa, apresentaremos uma situação onde dois médicos avaliam de forma independente o resultado de 180 exames de diagnóstico por imagem e o classificam como “normal”, “alterado” e “inconclusivo”.
Exemplo de aplicação do Coeficiente de Concordância de Kappa
Em nosso exemplo, poderíamos formar uma base de dados com a seguinte estrutura:
| Paciente | Médico X | Médico Y |
| 1 | Normal | Normal |
| 2 | Alterado | Inconclusivo |
| 3 | Inconclusivo | Normal |
| 4 | Alterado | Alterado |
| … | … | … |
Nesse caso poderíamos resumir os dados em uma tabela de contingência:
| Médico Y | Total | ||||
| Normal | Alterado | Inconclusivo | |||
| Médico X | Normal | 54 | 12 | 12 | 78 |
| Alterado | 6 | 24 | 12 | 42 | |
| Inconclusivo | 18 | 18 | 24 | 60 | |
| Total | 78 | 54 | 48 | 180 | |
Na primeira coluna da tabela de contingência, podemos ver que 54 resultados foram considerados normais pelos dois médicos, 6 foram considerados alterados pelo médico X e normais pelo médico Y e 18 foram considerados inconclusivos pelo médico X e normais pelo médico Y.
Considerando os resultados sintetizados na tabela de contingência, podemos afirmar que os dois médicos são concordantes na avaliação dos resultados dos exames de diagnóstico por imagem?
Cálculo do Coeficiente de Concordância de Kappa
A tabela de contingência utilizada no exemplo é um caso específico de uma tabela do tipo:
| Juiz Y | Total | |||||
| 1 | 2 | … | r | |||
| Juiz X | 1 | n11 | n12 | … | n1r | n1. |
| 2 | n21 | n22 | … | n2r | n2. | |
| … | … | … | … | … | … | |
| r | nr1 | nr2 | … | nrr | nr. | |
| Total | n.1 | n.2 | … | n.r | n | |
Onde:
- r representa as categorias de avaliação
- nij representa a quantidade de elementos amostrais avaliados pelo juiz X na categoria i e pelo juiz Y na categoria j
- n.i representa a quantidade de elementos amostrais avaliados pelo juiz Y na categoria i
- ni. representa a quantidade de elementos amostrais avaliados pelo juiz X na categoria i
- n representa o total de elementos amostrais avaliados.
O coeficiente de concordância de Kappa, sugerido por Cohen em 1960, é calculado utilizando a fórmula abaixo:
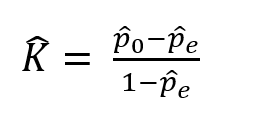
onde
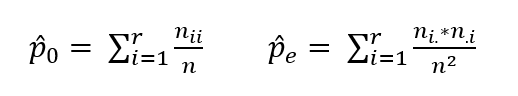
Sendo assim, em nosso exemplo:
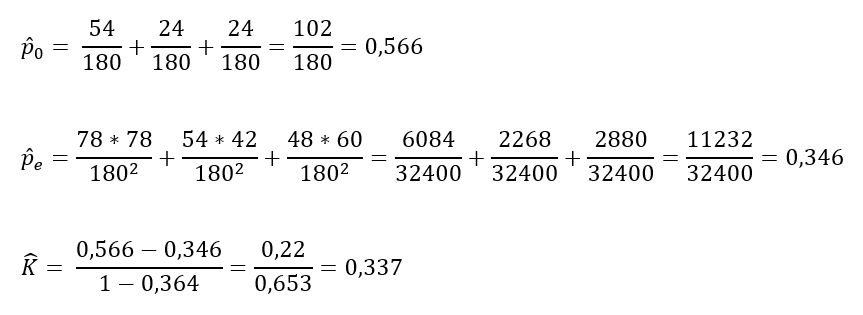
Em nosso exemplo, chegamos ao coeficiente de Kappa de 0,337. Mas o que isso significa?
Interpretando o Coeficiente de Concordância de Kappa
O valor do coeficiente de concordância de Kappa pode variar de (-pe/1-pe) até 1. Quanto mais próximo de 1 for seu valor, maior é o indicativo de que existe uma concordância entre os juizes e quanto mais próximo de zero, maior é o indicativo de que a concordância é puramente aleatória.
No artigo The measurement of observer agreement for categorial data, publicado na Biometrics em 1977 (disponível em http://www.jstor.org/stable/2529310) , os autores Landis JR. e Koch GG. sugerem uma tabela para interpretar o valor de Kappa.
| Valor de Kappa | Interpretação |
| Menor que zero | insignificante (poor) |
| Entre 0 e 0,2 | fraca (slight) |
| Entre 0,21 e 0,4 | razoável (fair) |
| Entre 0,41 e 0,6 | moderada (moderate) |
| Entre 0,61 e 0,8 | forte (substantial) |
| Entre 0,81 e 1 | quase perfeita (almost perfect) |
Eles ressaltam que embora essas divisões sejam claramente arbitrárias, elas podem fornecer uma referência útil para a discussão.
Para auxiliar na interpretação do resultado, utiliza-se um teste de hipóteses que testa a hipótese de que a concordância entre os dois médicos seja puramente aleatória.
Coeficiente de Concordância de Kappa no R
É possível obter o coeficiente de concordância de Kappa no R utilizando a função Kappa2 do pacote irr. Vamos ver como, utilizando o nosso exemplo.
Suponha que a base de dados lida pelo R possui o seguinte cabeçalho:
> head(dados) paciente medicoX medicoY 1 1 normal normal 2 2 alterado inconclusivo 3 3 inconclusivo normal 4 4 alterado alterado 5 5 normal normal 6 6 alterado alterado
Nesse caso é necessário organizar os dados em uma matriz com 2 colunas:
> dadoskappa<-cbind(dados$medicoX,dados$medicoY)
> head(dadoskappa)
[,1] [,2]
[1,] 3 3
[2,] 1 2
[3,] 2 3
[4,] 1 1
[5,] 3 3
[6,] 1 1
Observe que a matriz dadoskappa recodificou os valores das categorias em 1, 2 e 3.
Em seguida é necessário carregar o pacote irr e chamar a função kappa2 utilizando a matriz criada como argumento.
> library(irr)
> kappa2(dadoskappa)
Cohen's Kappa for 2 Raters (Weights: unweighted)
Subjects = 180
Raters = 2
Kappa = 0.337
z = 6.39
p-value = 1.67e-10
A função, além de apresentar o valor do coeficiente de concordância de Kappa, ainda apresenta op-valor do teste de hipóteses.
Com seu valor menor que 0,001, rejeitamos a hipótese de que a concordância entre os médicos foi puramente aleatória. Ainda, utilizando a interpretação proposta por Landis JR. e Koch GG., podemos afirmar que os dois médicos apresentaram uma concordância razoável em relação aos diagnósticos a partir dos exames de imagem.
Variações do Coeficiente de Concordância de Kappa
Também se pode calcular o coeficiente de concordância de Kappa para o caso em que há mais de dois juízes, conhecido como Kappa Múltiplo ou Kappa de Fleiss.
Além disso, também existe uma maneira de se ponderar as categorias por sua importância ou ainda ponderar de acordo com pesos dos elementos amostrais. Nesse caso, o coeficiente é chamado de Kappa Ponderado.
O Kappa Ponderado é indicado para os casos em que as categorias da avaliação são ordinais, como por exemplo ruim, médio e ótimo. Afinal se um juiz classifica como ruim e outro como ótimo, a discordância é maior do que se tivessem classificado como ruim e médio.
Poderemos abordar essas variações do coeficiente de Kappa em futuras publicações e também tratar sobre a concordância entre juízes quando a avaliação é quantitativa ao invés de qualitativa. Por esse motivo, não deixe de se inscrever em nosso blog para receber nossas futuras publicações.




5 comentários em “Coeficiente de Concordância de Kappa”
Olá boa noite,
Gostaria de saber se existe algum estudo com aplicação do método Kappa na Telemedicina ?
Desde já agradeço
Olá, gostaria de saber qual coeficiente usamos quando queremos avaliar a concordância de um mesmo avaliador, antes e depois (de um evento, por exemplo).
Oi Matheus! O teste usado quando queremos medir a concordância entre avaliadores antes e depois de um evento depende do tipo de dado. Se o dado for categórico, por exemplo, se estiver avaliando se uma coisa é positiva ou negativa e checando se as pessoas mudaram ou não de opinião, você deve usar o teste Kappa de Cohen. Já se você estiver medindo algo que é numérico, como uma nota de 1 a 10, pode fazer o Kappa Ponderado.
Olá, onde posso encontrar a calculadora on line para a concordância de Kappa?
Ei Maria, aqui na Oper nós confiamos mais no R do que em calculadoras online. Mas conversando com nossos data talkers eles sugeriram essas duas opções aqui
1. http://justusrandolph.net/kappa/ que é mais simples, rápida de usar e retorna apenas duas casas decimais.
2. http://vassarstats.net/kappa.html mais robusta, calcula para vários casos, retorna com mais casas decimais e pesos.
O problema é que nenhuma das duas indica valor-p.